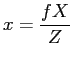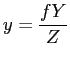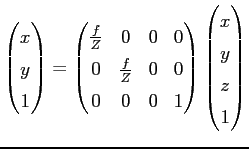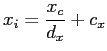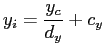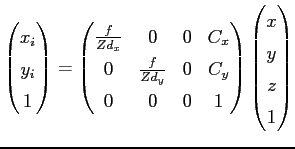Next: Camera Model with Lens
Up: Perspective Projection
Previous: Perspective Projection
The Pinhole Camera
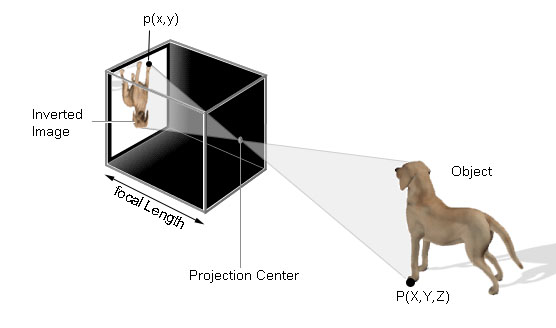
An ideal model of a camera is the pinhole camera, as seen in Figure 2.2. This kind of
camera can be imagined as a box with a pinhole, through which
light enters and forms a two-dimensional image on the opposite site. A point
![]() in the three-dimensional
in the three-dimensional ![]() -space is projected to an image-point
-space is projected to an image-point
![]() in the two-dimensional
in the two-dimensional ![]() -space (wall). If the coordinate system of the
-space (wall). If the coordinate system of the
![]() -space is aligned at the pinhole so that the Z-axis coincides with the optical axis and the image
-space is aligned at the pinhole so that the Z-axis coincides with the optical axis and the image
plane has its origin at ![]() , then the projection equations are
, then the projection equations are
given by
To represent Equation 2.4 and Equation 2.5 in a linear way, we transform the point ![]() in the Euclidean plane to a point
in the Euclidean plane to a point ![]() in the projective plane. This represents the same point, we simply added a new coordinate
in the projective plane. This represents the same point, we simply added a new coordinate ![]() . Overall scaling is unimportant. The point
. Overall scaling is unimportant. The point
![]() can be re-transformed by dividing through
can be re-transformed by dividing through ![]() . Thus
. Thus ![]() is similar to
is similar to
![]() . Because scaling is unimportant, the coordinate
. Because scaling is unimportant, the coordinate ![]() is called homogeneous coordinate. Homogenous coordinates can also be used within a higher dimensional domain. Now we can combine Equation 2.4 and Equation 2.5 to
is called homogeneous coordinate. Homogenous coordinates can also be used within a higher dimensional domain. Now we can combine Equation 2.4 and Equation 2.5 to
If we want to know the image coordinates we have to take four more values into account. Namely

- image principal point, which is the intersection between the camera’s optical axis and the image plane.

- distance between two sensor elements in
 and
and  direction
direction
![]() and
and ![]() can normally be found in the datasheet2.2 of the sensor chip. The image principal point has to be found by calibration (see Section 2.2 for more information). If the parameters and the point in camera coordinates are known, we can compute the image coordinates with the following formulation
can normally be found in the datasheet2.2 of the sensor chip. The image principal point has to be found by calibration (see Section 2.2 for more information). If the parameters and the point in camera coordinates are known, we can compute the image coordinates with the following formulation
Next: Camera Model with Lens
Up: Perspective Projection