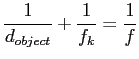Anagram Engineering

Webdesign und Softwarelösungen aus Vorarlberg. Ihr Partner für innovative Lösungen rund ums Internet. Full Service Agentur.

Camera Model with Lens



Next: Camera Calibration
Up: Perspective Projection
Previous: The Pinhole Camera


Camera Model with Lens

The pinhole camera has the problem that the pinhole should be almost infinitely small, but the smaller the pinhole, the fewer light enters the camera and the longer exposure time is needed. In a dynamic environment this is not possible because the objects in the scene are moving. As a result the pinhole camera is not used in real photography. In reality lenses are used to project the light onto the sensor chip. Figure 2.3 shows how the light-rays reflected by an object are projected through a lens. $ G$ is an object in the real world,
$ d_{object}$ is the distance between $ G$ and the lens. $ f$ is the focal distance of the lens, $ f_k$ is the effective focal length (distance between the lens and the projected object $ B$) and $ B$ is the projected object. Light is reflected at the object $ G$ and some of the light-rays enter the lens where they are refracted towards the sensor plane and form the object $ B$. The relation between these parameters can be written in a mathematical form.


As a result of Equation 2.10, the focal length of the lens and the effective focal length are only the same if an object infinitely far away is focused. For reconstruction,
$ d_{object}$ has to be approximated, thus the effective focal length has to be computed. As one can see in Equation 2.10, $ f_k$ strongly depends on the focused objects and should be chosen so that the objects of interest are focused. Objects that are closer or further away will not be mapped as points but as circles. This happens because the correct image point lies behind or in front of the image plane. Areas which are not focused thus look blurred. There are some general laws which can help choosing the correct lens for a given problem.

  • the bigger the aperture, the bigger are the circles
  • the smaller the aperture, the sharper is the whole scene
  • the bigger the depth sharpness, the lesser light arrives at the sensor chip
  • the bigger the aperture, the smaller is the area where objects are mapped sharp

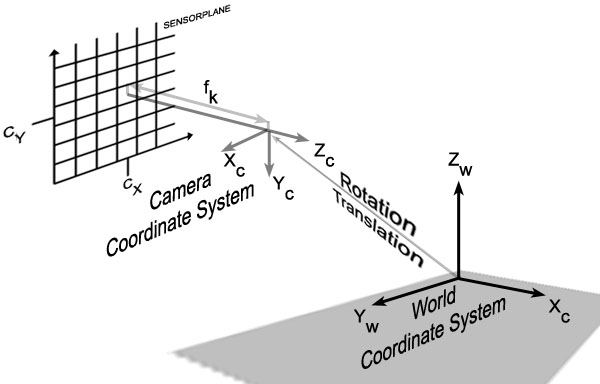
Camera parameters can be used to describe the camera geometry. It can be distinguished between two groups of parameters, namely the interior and exterior camera parameters. The interior parameters describe the camera geometry, independently from where the camera is situated. The exterior camera parameters depend only on the position where the camera is placed in relation to a given world coordinate system. Camera calibration is needed to compute both, the interior and the exterior camera parameters.

The intrinsic parameters are

and they determine the geometrical behavior of the projection
caused by the lens used. The extrinsic parameters are

When a lens is used, it comes to geometric lens distortion which has no influence on the quality of the image, but it has a significant influence on the image geometry. There are two kinds of geometric distortion, radial and tangential, but radial distortion is the most general. Figure 2.5 shows the effects of radial distortion to the image geometry. It can be described as a radial outwards or inwards displacement of a point in reference to the midpoint (principle point) of the lens. Some radial distortion is inherent in most optical systems, but can be reduced by proper design. Figure 2.5a shows the effect of inwards displacement(barrel distortion). Figure 2.5b shows the effect of outwards displacement (pincushion distortion).

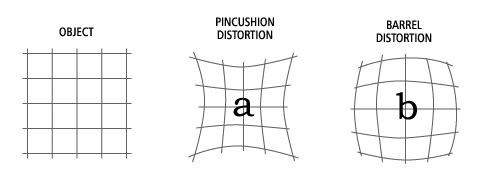The distortion coefficients
$ kappa_1,kappa_2$ describe the radial distortion and can be found using one of the calibration techniques presented in Section 2.2. Some implementations also deal with tangential distortion, even if it is often disregarded due to its negligible influence.

Next: Camera Calibration
Up: Perspective Projection