Next: Summary
Up: Stereo Vision
Previous: Feature-based Correspondence Analysis
3D Reconstruction
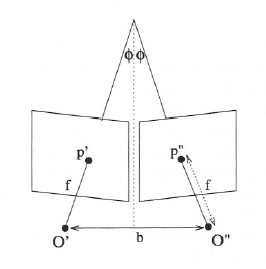
After the calibration is done and corresponding features in both images are found, the 3D position of the feature can be computed. With an intensity based approach a dense disparity map can be generated. A feature-based approach only provides disparity information for the features that have been extracted. Interpolation can be used to get more 3D points. The mathematical formulation to get the coordinates of an image point in the camera coordinate system2.4 is given by
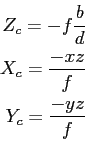 |
The angle between the optical axes is 2![]() . The y-axis of the camera coordinate system has to be parallel. The relation between a point
. The y-axis of the camera coordinate system has to be parallel. The relation between a point
![]() in the cyclopean coordinate system, and the same point
in the cyclopean coordinate system, and the same point
![]() can be written as
can be written as
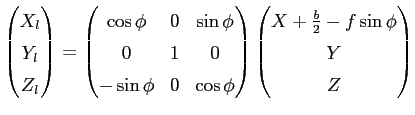 | (2.37) |
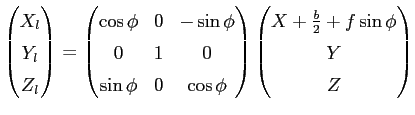 | (2.38) |
 | (2.39) |
Next: Summary
Up: Stereo Vision