Next: Fundamental Matrix
Up: Stereo Geometry
Previous: Stereo Geometry
Epipolar Geometry
The epipolar geometry is the intrinsic projective geometry between two views. It is independent of scene structure, and only depends on the camera’s internal parameters and relative pose. The fundamental matrix ![]() encapsulates this intrinsic geometry. It is a
encapsulates this intrinsic geometry. It is a ![]() matrix of rank 2. If a point
matrix of rank 2. If a point ![]() in space is mapped to one image as
in space is mapped to one image as ![]() , and to the second image as
, and to the second image as ![]() , then the image points satisfy the relation
, then the image points satisfy the relation
![]() .
. ![]() can be computed if both camera parameters are known. More about this in Section 2.3.2.
can be computed if both camera parameters are known. More about this in Section 2.3.2.
The relation between a projected point ![]() in one’s view and its corresponding point
in one’s view and its corresponding point ![]() in the other view can be described geometrically. In Figure 2.7, we can see that for every point
in the other view can be described geometrically. In Figure 2.7, we can see that for every point ![]() a corresponding line, on which
a corresponding line, on which ![]() can be found, exists. These lines are called epipolar lines. The intersection between the baseline
can be found, exists. These lines are called epipolar lines. The intersection between the baseline ![]() and the image planes is called epipole. All epipolar lines intersect at the epipole.
and the image planes is called epipole. All epipolar lines intersect at the epipole.
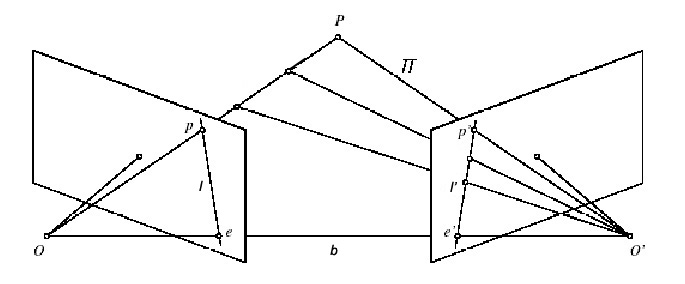 |
If a point ![]() in space is known, the corresponding epipolar lines can be found by computing the intersection between the two image planes, and the plane that is formed by the baseline
in space is known, the corresponding epipolar lines can be found by computing the intersection between the two image planes, and the plane that is formed by the baseline ![]() and the line from the optical center
and the line from the optical center ![]() to the point
to the point ![]() . In Figure 2.7 the epipolar lines are denoted by
. In Figure 2.7 the epipolar lines are denoted by ![]() and
and ![]() . Supposing now that we know only
. Supposing now that we know only ![]() , we may ask how the corresponding point
, we may ask how the corresponding point ![]() can be found. The plane
can be found. The plane ![]() is determined by the baseline and the ray defined by point
is determined by the baseline and the ray defined by point ![]() . From above we know that the point
. From above we know that the point ![]() lies inside the line
lies inside the line ![]() which is the intersection of plane
which is the intersection of plane ![]() with the second image plane. In terms of a stereo correspondence algorithm the benefit is that we do not have to search the entire image for the corresponding point
with the second image plane. In terms of a stereo correspondence algorithm the benefit is that we do not have to search the entire image for the corresponding point ![]() but only along the line
but only along the line ![]() . The fundamental matrix
. The fundamental matrix ![]() is the algebraic representation of the epipolar geometry and is discussed in the next section.
is the algebraic representation of the epipolar geometry and is discussed in the next section.
Next: Fundamental Matrix
Up: Stereo Geometry
